When I was an undergraduate student, I tried to use OpenCV for some purposes. But I gave up because it required a high level of programming skills in order to understand how the library works. Especially Visual C++ needs specific settings, such as /clr:pure to /clr in the option of common language runtime. OpenCV is written in C++. On the other hand, the default settings of Visual C++ accepts only C++/CLI, which is a kind of managed language looking like C++.
In addition to my poor skills, some functions has been apparently replaced with new ones when its version was changed to 2.x. For example, "imread" is used to load an image file while "cvLoadImage" has been used previously. I am afraid that it may be easy for other people to understand and use it, but I was actually confused.
However, I recently started to read the tutorial for ver 2.3. I feel that I will be finally able to understand its structure.
http://opencv.itseez.com/
One of the points I was surprised is that "IplImage" structure is no longer needed in the new version because "Mat" structure treats both images and matrices. I think Mat makes it easy to treat images. Actually, I can use openCV on Visual C++ now although I had many troubles with the old structures before using the new features.
2/23/2012
2/07/2012
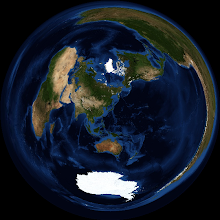
New program making azimuthal maps
I have been in work for applications to graduate schools. So I am considerably nervous!
While I was busy, I was also making a program projecting azimuthal maps.
I made a previous version a few years ago, but it was not good because it took SEVERAL MINUTES to project a map.
In the last month, I hit upon a good idea to make it fast and gathered related necessary techniques.
The new program takes only 100 milliseconds! (but I think that this implementation actually owes to Marshal class of .Net rather than my idea...)
I will upload my program and explain the calculation in my web site.




While I was busy, I was also making a program projecting azimuthal maps.
I made a previous version a few years ago, but it was not good because it took SEVERAL MINUTES to project a map.
In the last month, I hit upon a good idea to make it fast and gathered related necessary techniques.
The new program takes only 100 milliseconds! (but I think that this implementation actually owes to Marshal class of .Net rather than my idea...)
I will upload my program and explain the calculation in my web site.
The world (azimuthal equidistant projection)

Around Japan (azimuthal equidistant projection)

The pacific ocean (azimuthal equidistant projection)

The world (azimuthal equal-area projection)

Subscribe to:
Posts (Atom)